Obliczenia kondensatora metodą elementów skończonych (MES, FEM) na przykładzie programu FreeFem
Kondensator opis
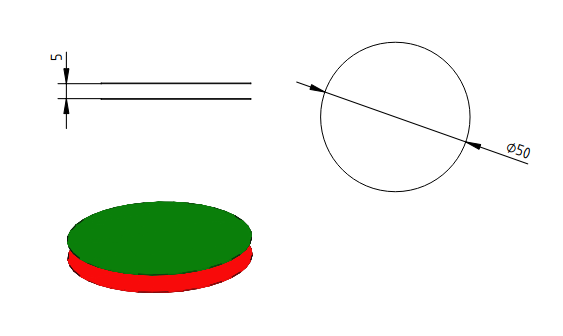
Kondensator jest elementem przechowującym energię w polu elektrycznym. Na rysunku powyżej jest najprostsza jego wersja, kondensor powietrzny, którego pojemność można obliczyć ze wzoru:
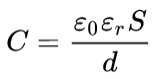
gdzie:
C - pojemność, F
ε0 - przenikalność elektryczna próżni, 8,84·10−12 F/m
εr - względna przenikalność dielektryczna
S - powierzchnia okładki, m, np S=πR2 (R - promień okładki)
d - odległość między okładkami, m
| Średnica, mm |
|
50mm |
| odległość między okładkami |
|
20mm |
| względna przenikalność dielektryczna (domyślna wartość dla powietrza) |
|
20 |
| Pojemność kondensatora, C |
= |
20 |
Lub dla z dokładniejszego wzoru dla kondensatora powietrznego, gdy elektrody są okrągłe:
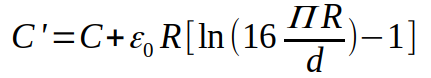
gdzie:
C - jest wartością z "podstawowego" wzoru, F
R - promień, m
d - odległość między okładkami. m
Dla elektrod kwadratowych:
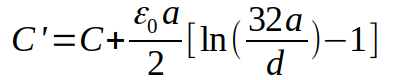
gdzie:
C - jest wartością z "podstawowego" wzoru, F
a - długość boku, m
d - odległość między okładkami. m
Przygotowanie geometrii
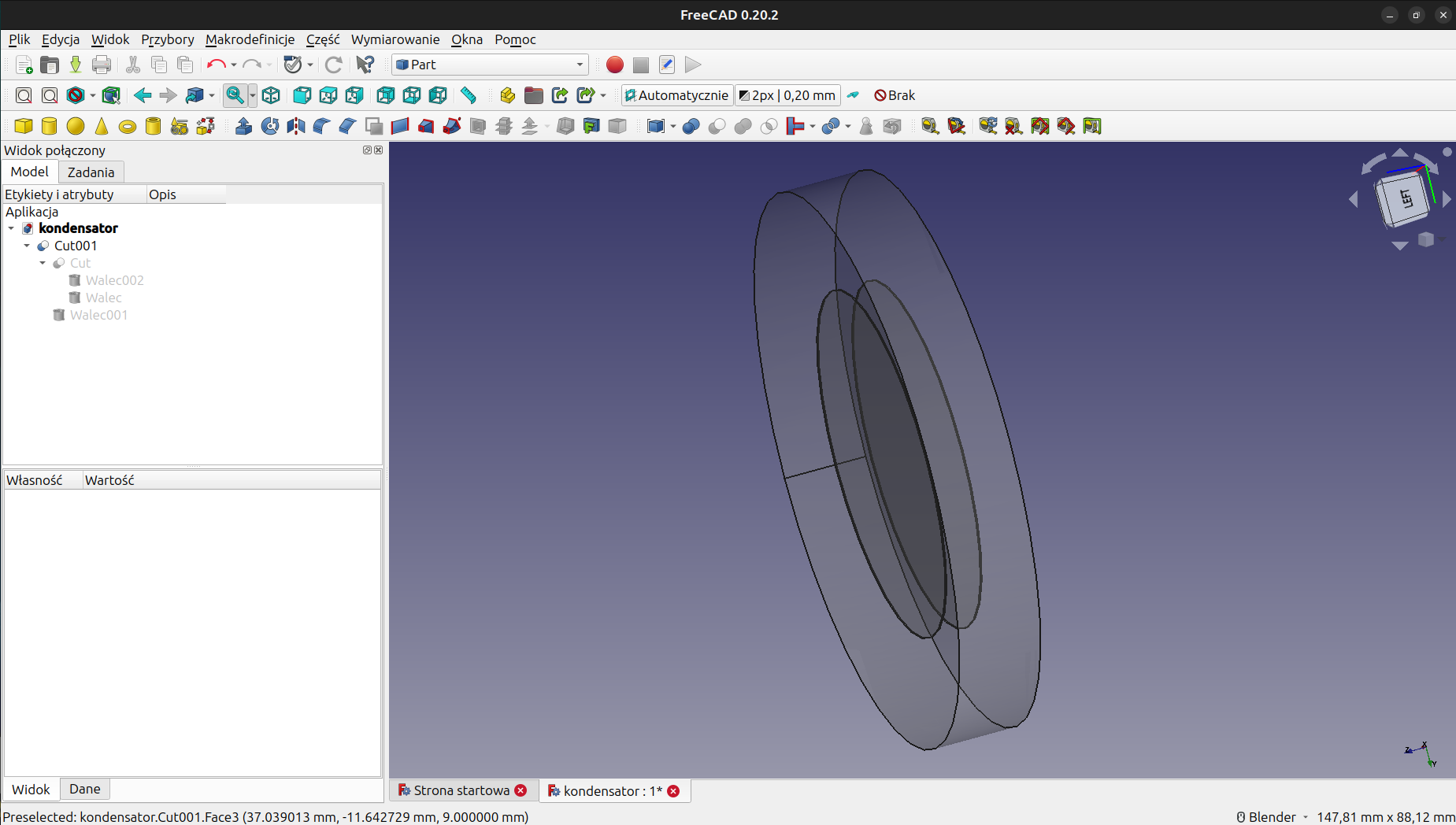
Geometrię można przygotować w programie do obliczeń. Program FreeFem posiada możliwość tworzenia geometrii, jest to mocno czasochłonne. Wygodniejszym sposobem jest skorzystanie z programu Cad, w tym przypadku zastosowałem FreeCad (nazwy zbliżone, są to odrębne programy). Można stosować dowolny program, zaletą freecad-a jest ogólna dostępność na wszystkie popularne systemy operacyjne i jego fakt, że jest darmowy. Jest to program który w wielu kwestiach odstaje od komercyjnych, ale jest to narzędzie potrafiące wiele. Na rysunku poniżej został zastosowany moduł "part", stworzyłem trzy walce. Od największego odjąłem dwa mniejsze, i zapisałem do pliku "step". Do nauki programu polecam kanał "Inżynier programista", autor szeroko opisał różne możliwości wspomnianego cad-a.
Przygotowanie siatki
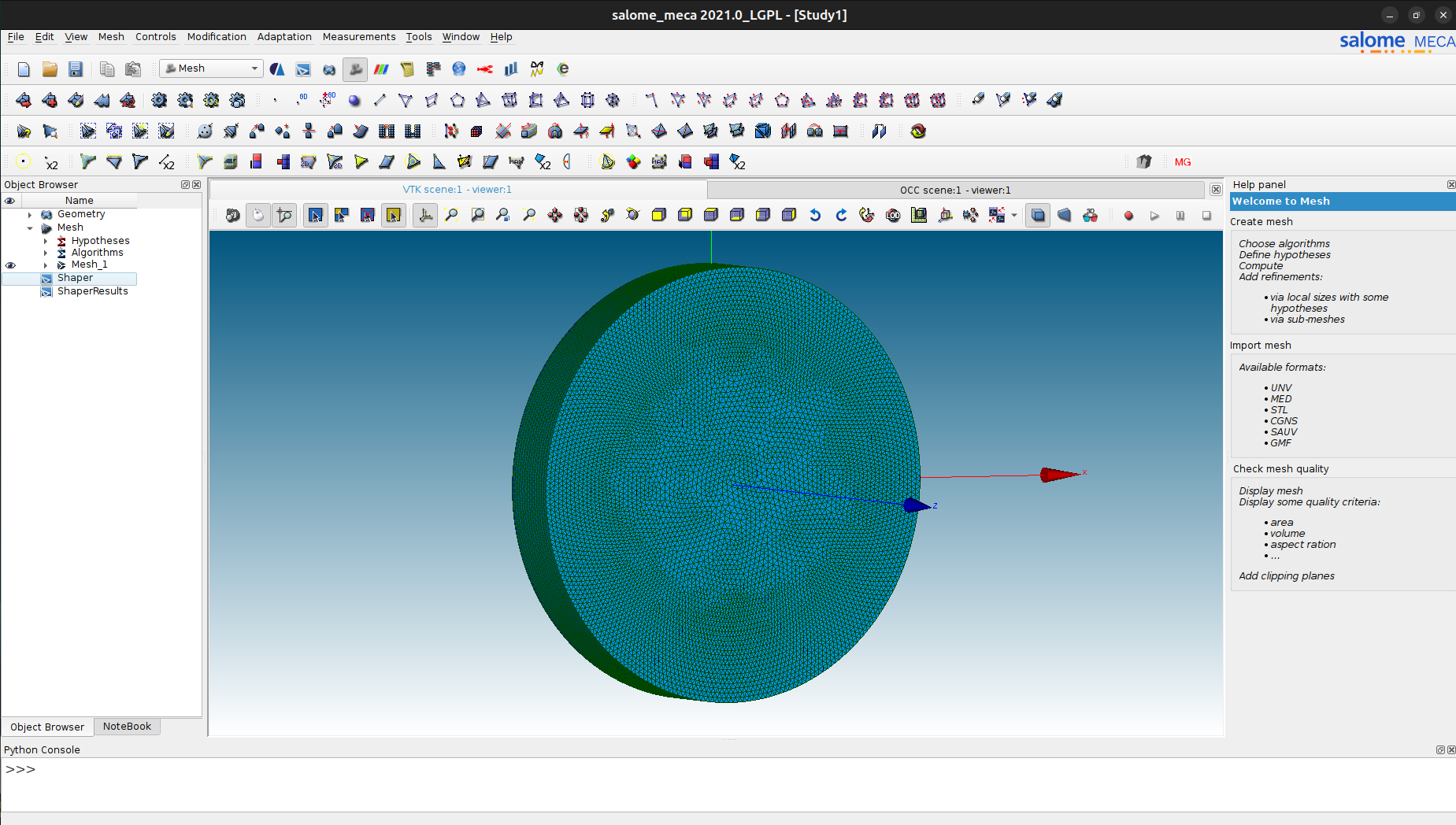
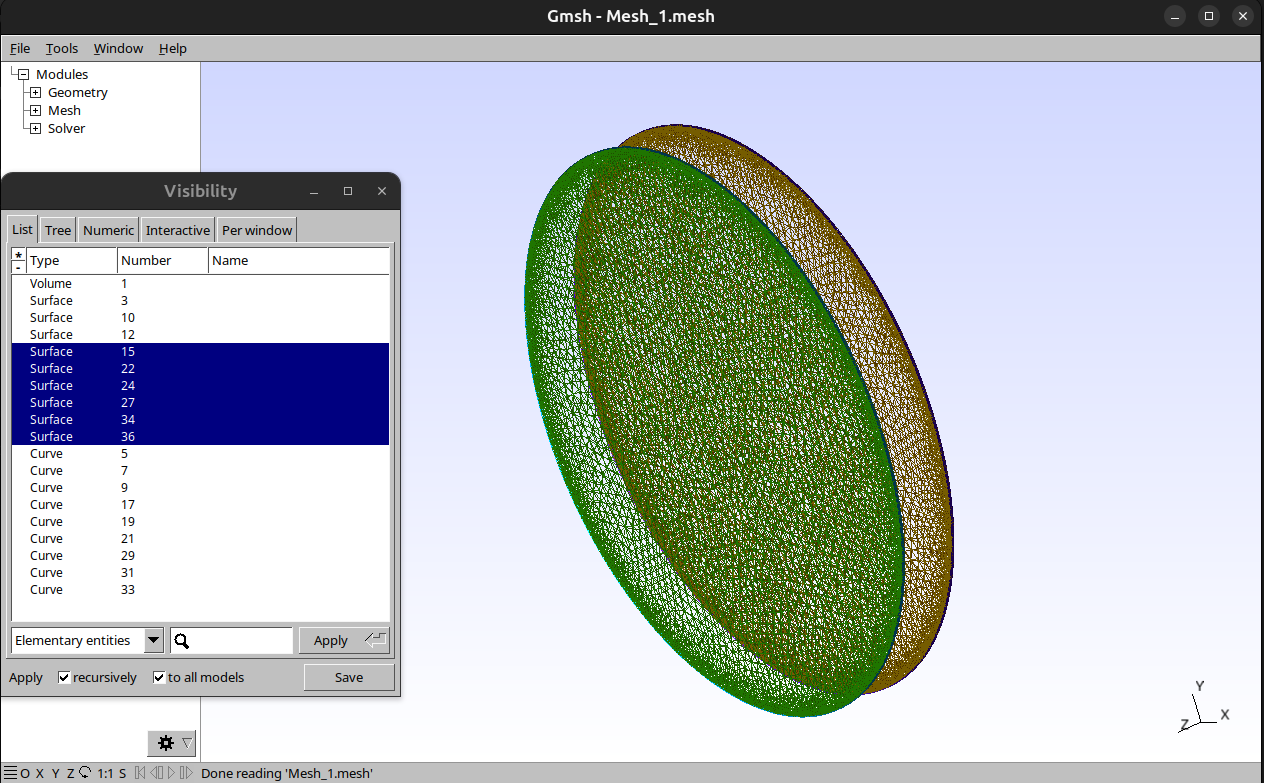
Do przygotowania siatki posłużył program salome-meca, rózni się ona od samego "salome" zintegrowaniem z "aster" - służy on do różnego typu obliczeń metodą elementów skończonych. Stworzona siatka została exportowana do pliku "GMF ascii" o nazwie "Mesh_1.mesh".
Kod w programie FreeFem
Słaba forma równania ("weak form") które będzie nam potrzebne wygląda jak poniżej:
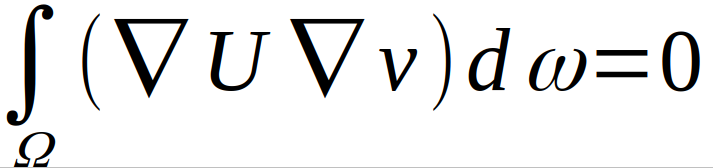
W zapisie freecad-a będzie to "int3d(Th)( dx(u)*dx(v) + dy(u)*dy(v) + dz(u)*dz(v) )". Lub zdefiniować makro Grad i zastosować "int3d(Th)( Grad(u)'*Grad(v) )". "on " w kodzie jest odpowiedzialne za wartości brzegowe. Np. on(24, u=U1) to powierzchnia 24 gdzie wartość u rest równa wartości w zmiennej U1. Poniższy kod wykonuje obliczenia i zapisuje je w formacie dla paraview.
load "msh3" // import biblioteki, stąd funkcja readmesh3
load "iovtk" // import biblioteki do zapisu w formacie paraview, nie potrzebne do samych obliczeń pojemnosci
mesh3 Th=readmesh3("./Mesh_1.mesh"); // wczytanie siatki
real U1 = 1; // napięcia na okładkach zapisane w zmiennych
real U2 = 0;
//plot(Th, wait=true); // okno z siatka, w tym momencie nie używane
fespace Vh(Th, P1);
Vh u, v;
macro Grad(u) [dx(u) ,dy(u), dz(u)]
// Problem
solve a(u, v)
= int3d(Th)(
Grad(u)'*Grad(v)
)
+ on(24, u=U1) // wybrano wszystkie powierzchnie, dla uproszczenia można wybrać po jednej z okładek
+ on(15, u=U1)
+ on(22, u=U1)
+ on(34, u=U2)
+ on(27, u=U2)
+ on(36, u=U2);
real e0 = 8.854e-12;
real er = 1.00054;
Vh Ex = -dx(u);
Vh Ey = -dy(u);
Vh Ez = -dz(u);
Vh E = (Ex^2 + Ey^2 + Ez^2)^0.5;
Vh envol = (x<25)*(x>-25)*(y<25)*(y>-25)*(z<5)*(z>0);
real energy = 0.5* e0 * er*int3d(Th) (envol*E^2);
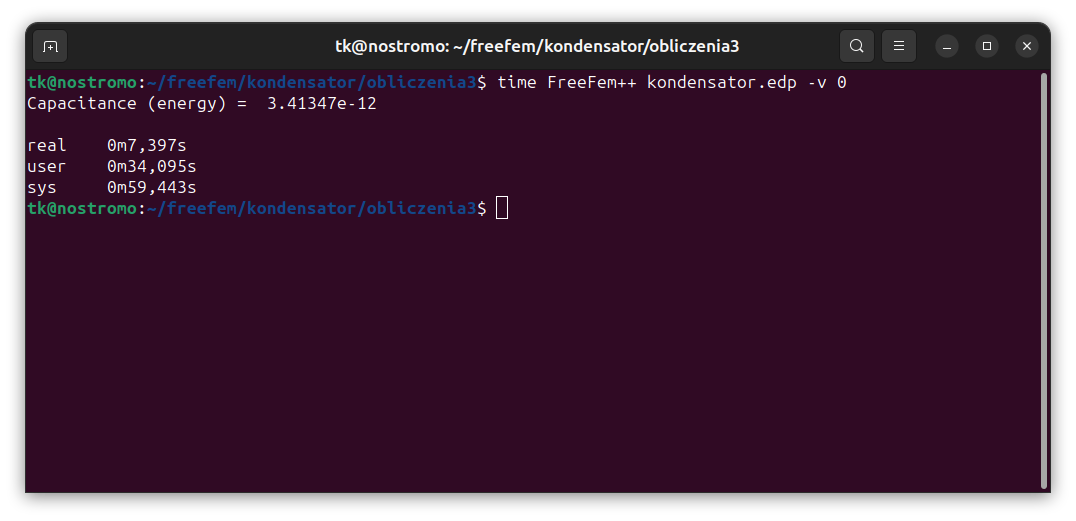
cout << "Capacitance (energy) = " << 2.0e-3*energy/((U1-U2)^2) << endl;
Vh Dx = e0*er*Ex;
Vh Dy = e0*er*Ey;
Vh Dz = e0*er*Ez;
Vh D = (Dx^2 + Dy^2 + Dz^2)^0.5;
int[int] Order = [1];
string DataName = "u";
savevtk("D.vtu", Th, [Dx, Dy, Dz], dataname=DataName, order=Order);
//plot(E, value=true, ps="condersor.eps");
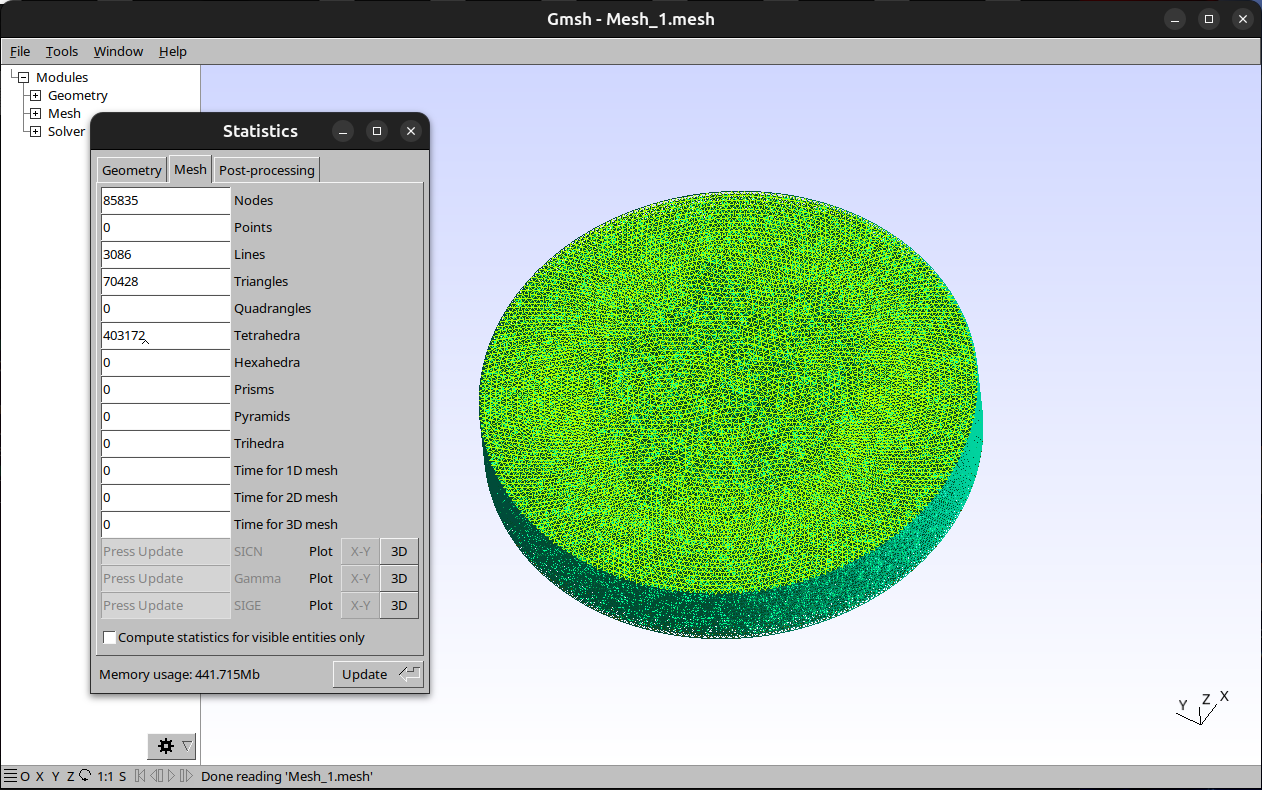
Numery powierzchni można podejrzeć w porogamie gmsh.
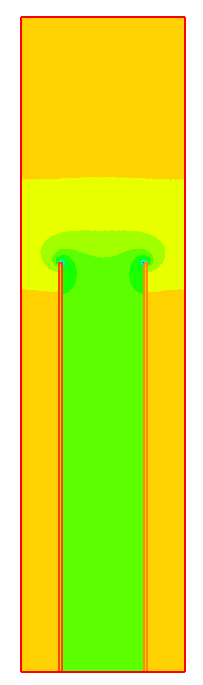
Wynik
Program uruchamia się za pomocą polecenia "FreeFem++" i podaje nazwę pliku. Opcja "-v 0" zmniejsza ilość wypisywanych danych, w tym przypadku ogranicza je praktycznie do wyniku. Polecenie "time" służy do pomiaru czasu działania programu (w tym przypadku jeden rdzeń na AMD Ryzen™ 9 PRO 3900 × 24, DDR4 32GB, siatka tetrahedra 403172).
Plik "D.vtu" można otworzyć za pomocą programu paraview.

Wersja programu 2D
Wersje 2D wykonano w całości w FreeFem. C01-08 to linie definiujące przestrzeń. C11-13 to linie anody. C21-23 to katoda. W tej wersji int3d zostało zamienione na int2d. Zmieniona macro Grad(u) na wersje 2D. Przy obliczeniach energi trzeba uwzględnić, że przypadek jest osiowo symetryczny, stąd int2d(Th)(2*pi*y*envol*E^2).
real pi = 3.14159265359;
int out = 1;
int anoda = 2;
int katoda = 3;
real U1 = 1;
real U2 = 0;
real h = 40;
real w = 10;
real g = 0.2;
real R = 50/2;
real d = 5;
real w1 = w/2-d/2-g;
real w2 = w/2-d/2;
real w3 = w/2+d/2;
real w4 = w/2+d/2+g;
border C01(t=0, 1){x=0; y=h*t; label=out;}
border C02(t=0, 1){x=w*t; y=h; label=out;}
border C03(t=0, 1){x=w; y=h-h*t; label=out;}
border C04(t=0, 1){x=w4+(w-w4)*t; y=0; label=out;}
border C05(t=0, 1){x=w3+(w4-w3)*t; y=0; label=out;}
border C06(t=0, 1){x=w2+(w3-w2)*t; y=0; label=out;}
border C07(t=0, 1){x=w1+(w2-w1)*t; y=0; label=out;}
border C08(t=0, 1){x=w1*t; y=0; label=out;}
border C11(t=0, 1){x=w1; y=R*t; label=anoda;}
border C12(t=0, 1){x=w1+(w2-w1)*t; y=R; label=anoda;}
border C13(t=0, 1){x=w2; y=R-R*t; label=anoda;}
border C21(t=0, 1){x=w3; y=R*t; label=katoda;}
border C22(t=0, 1){x=w3+(w4-w3)*t; y=R; label=katoda;}
border C23(t=0, 1){x=w4; y=R-R*t; label=katoda;}
int n = 1000;
//plot(C01(-n) + C02(-n/4) + C03(-n) + C04(n) + C05(n) + C06(n) + C07(n) + C08(n) + C11(n) + C12(n) + C13(n) + C21(n) + C22(n) + C23(n), wait=true);
mesh Th = buildmesh(C01(-n) + C02(-n/4) + C03(-n) + C04(n/10) + C05(n/10) + C06(n/4) + C07(n/4) + C08(n/10)
+ C11(n) + C12(n/15) + C13(n)
+ C21(n) + C22(n/15) + C23(n));
//plot(Th, wait=true);
fespace Vh(Th, P1);
Vh u, v;
macro Grad(u) [dx(u) ,dy(u)]
// Problem
solve a(u, v)
= int2d(Th)(
Grad(u)'*Grad(v)
)
+ on(anoda, u=U1)
+ on(anoda, u=U1)
+ on(anoda, u=U1)
+ on(katoda, u=U2)
+ on(katoda, u=U2)
+ on(katoda, u=U2);
real e0 = 8.854e-12;
real er = 1.00054;
Vh Ex = -dx(u);
Vh Ey = -dy(u);
Vh E = (Ex^2 + Ey^2)^0.5;
//plot(E, value=true, ps="E.eps");
Vh envol = (x>w2)*(x < w3) * (y>0)*(y < R);
//Vh envol = 1;
real energy = 0.5* e0 * er*int2d(Th) (2*pi*y*envol*E^2);
cout << "Capacitance (eq) = " << er*e0*(pi*(R*1e-3)^2)/(d*1e-3) << endl;
cout << "Capacitance (energy) = " << 2.0e-3*energy/((U1-U2)^2) << endl;
Vh Dx = -e0*er*dx(u);
Vh Dy = -e0*er*dy(u);
Vh D = (Dx^2 + Dy^2)^0.5;
cout << "Number of triangle(s) = " << Th.nt << endl;
//plot(D, value=true, ps="D.eps");
Zmieniając wartość w zmiennej n zmienia wielkość siatki. Pomiżej wynik dla n=500 i n=1000.
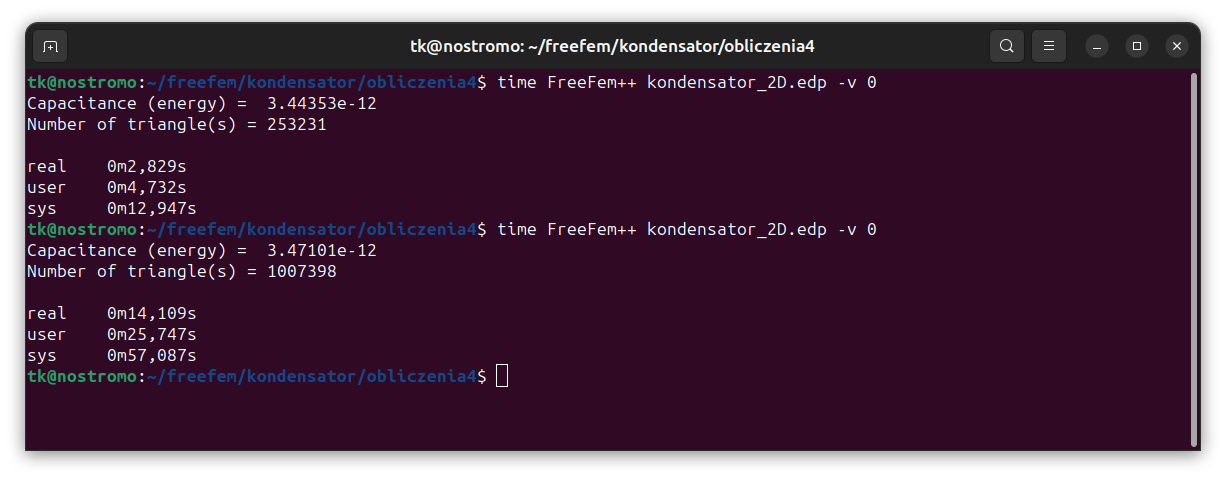
Wyniki dla D: